In researching the earlier post A Non-Math Look at Math Objects, I found that there is what a non-math person like me would call an infinite number of strange terms in geometry and topology that refer to shapes, objects, and patterns both imaginary and usable in the real world. Someone who is not used to this kind of higher thinking can only absorb so many of them at a time! Here are seven more.
Hyperboloid
What mathematicians call a hyperboloid of one sheet is a really cool structure that is made up of many (actually an infinite number) of perfectly straight lines that look to us like a curved structure. First, imagine that you have a cube. Stand it on one of its corners and spin it like a top, then look at it from the side -the sides seem to be curved, but you know they aren't. Now, take a handful of uncooked spaghetti noodles. Use two hands, and twist the strands loosely. It forms the shape of a hyperboloid structure, which looks like a cooling tower at a nuclear reactor. All the spaghetti noodles are still straight, but the shape of the handful is curved. In architecture, this idea enables builders to produce curved structures by using straight line supports.
Apollonian Gasket

An Apollonian gasket is a fractal generated when you mash as many round soap bubbles together as you can. At least, that's what it looks like. The pattern is based on threes: every circle touches two other circles. As you add more circles in the smaller spaces, they also touch two existing circles (and eventually many smaller ones). The number of smaller circles that can be added is mathematically infinite. Frothing soap bubbles can help us picture the Appolonian gasket, but the analogy is flawed, because real world soap bubbles do not like empty spaces. There is a limit to the volume of soap, and surface tension will connect round bubbles and flatten them against each other. This fractal is named for the ancient Greek mathematician Apollonius of Perga. The 3-dimensional fractal of this sort is called the Apollonian sphere packing, which is a pretty descriptive name for a math term.
Möbius Strip
When I was very young, first or second grade, my father told me he could make a piece of paper with only one side. Then he took a strip of paper, gave one end a half-twist, and taped the ends together. Then he showed me how he could draw one line down the strip without stopping and it covered the whole strip, no matter which way you turned it! I couldn't wait to show the Möbius strip to my friends at school. When I did, they just stared at me and told me I was weird.
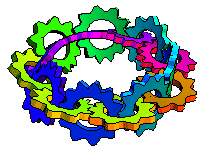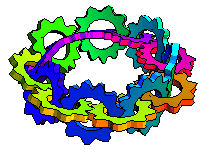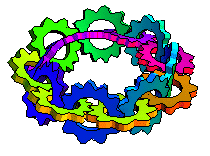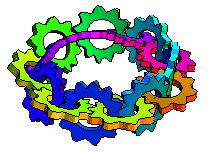
Maybe "continuous plane" is a better description than "one sided paper". The Möbius strip is named for August Ferdinand Möbius who discovered it in 1858. Johann Benedict Listing also came up with the concept around the same time and actually published his work, but maybe someone thought calling it a "Listing strip" would be confusing. Anyway, the Möbius strip does have some real-world applications. For example, conveyor belts and recording tapes with a half-twist last twice as long as they would otherwise because the entire surface is used instead of just one side of a two-sided strip. It's also an attention-getter in art and even architecture.
Klein Bottle
The Klein bottle came about from an attempt to make a 3-dimensional Möbius strip. In 1882, mathematician Felix Klein theorized about a container that had no inside or outside -just one "side"- in this manner:
Take a rectangle and join one pair of opposite sides -- you'll now have a cylinder. Now join the other pair of sides with a half-twist. That last step isn't possible in our universe, sad to say. A true Klein Bottle requires 4-dimensions because the surface has to pass through itself without a hole.
Here in the real (3-dimensional) world, we cheat by passing the neck of the bottle through itself using a real hole. You can see that process in sequence. You can see (and purchase) the finished product. You can put water into a Klein bottle (carefully), but you can't see a defined lip, meaning there is no discrete border between what is the inside and what is the outside of the container.
The Heliospheric Current Sheet
The Heliospheric current sheet is the shape of the sun's magnetic field. As the sun rotates, the magnetic field is forced into a spiral, called a Parker Spiral. The spiral has four arms with two different polar phases. As these rotate, the shape of the current sheet (which is the effect of the magnetic field on the plasma in the solar wind) forms a 3-dimensional spiral that resembles a twirling dancer with a voluminous skirt. Picture the bottom polarity as the dancer pushing her skirt down (with two hands) while the force of the twirl raises it like the upper polarity does. The two different polarities causes the vertical shape and the outward spiral causes the horizontal shape. You can reproduce this shape by twirling around while holding a gushing garden hose. Be sure to move the hose up and down as you turn -or better yet, watch while someone else does all this.
Vesica Piscis
The words vesica piscis literally translates to English as fish bladder. It is the name of the particular shape created when two circles of the same size overlap so that the edge of each circle touches the center of the other, such as the shape you see in the middle part of a two-circle Venn diagram. You could easily say this is just two identical curves placed together, but those curves have a lot of symbolism, going back to ancient times. The two curves with a bit of the crossover left on in the shape of a fish were used as a symbol of Christianity in its early days (and today as well). The shape is also the basis of the Gothic arch, which is stronger than a regular round arch in that it resists pressure from the sides as well as from above. It enabled architects to build huge structures with taller but stable doors and windows. The vesica piscis is also symbolic of the overlapping visual field of our two eyes -and, of course, some see it as a vagina.
Buddhabrot
Pareidolia is the tendency of humans to see meaningful shapes in everyday objects, like the image of the Virgin Mary in a grilled cheese sandwich. In studying the Mandelbrot set of fractals, which we looked at the in the previous post, several people noticed that if you turned the traditional rending of the fractal on its side, the shape looks like a sitting Buddha. This led to the search for the precise formula to generate a Buddhabrot. Turn your head to left while looking at this image and try to tell me you don't see a golden statue. The number of iterations (how many fractal levels are rendered to be visible) has a lot to do with the shape you see. As in the previous post, you can get a much more mathematical explanation of each of these shapes, including formulas, by clicking on the links in this post.









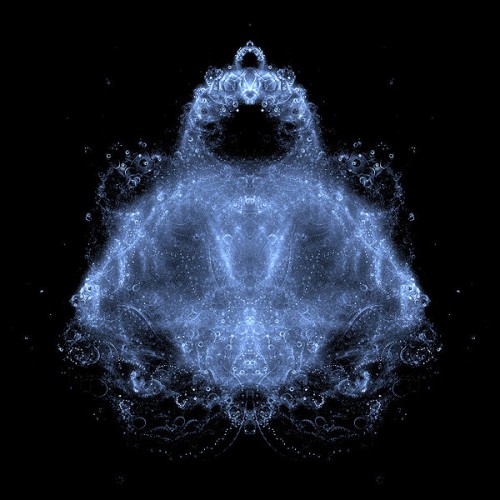





Comments (5)
http://www.cambridge2000.com/gallery/images/P32019262e.jpg
do with the mobius gears.
The Mobius strip cannot double the lenght of a conveyor belt though. As your source says, they made conveyor belt that way so that each side wears evenly.
The Mobius strip cannot double the lenght of a conveyor belt though. As your source says, they made conveyor belt that way so that each side wears evenly.
do with the mobius gears.
http://www.cambridge2000.com/gallery/images/P32019262e.jpg