A Non-Math Look at Math Objects

I found out something neat about three-dimensional shapes. Many strange mathematical solids are constructed by rotating the plane of a two-dimensional shape around an imaginary axis. Think of the flat holiday decorations you fold out around its spine/axis. Once I understood what is called a “surface of revolution” in my mind, the construction of many odd mathematical shapes began to make sense.

Superegg

(Image credit:  Sir48 at da.wikipedia)

A superegg is a mathematical shape constructed by rotating a superellipse around an axis to the formula of |x/a|2.5 + |y/b|2.5 = 1, where a/b = 4/3. (If you search for “superegg formula”, you are liable to find something completely different.) But you don’t want to bother with formulas, do you? Just look at it! From the side, the superegg looks a bit like a cylinder, but has no corners. If you cut one horizontally, the cross-section will be a circle. However, unlike a natural egg, you can stand the superegg on its end -either end, as a matter of fact, as it is vertically as well as horizontally symmetrical, although it has no straight lines that you can find -although the curvature is zero at the ends, the “ends” are actually quite small and appear to be rounded. The superegg was popularized by Danish mathematician and physicist Piet Hein, who used the shape in designs for household items such as furniture, ice cubes, and candles, as well as a novelty toy (sometimes referred to as a stress-reliever) by itself.

Torus

I learned about the torus from crossword puzzles. If the clue says “donut shape”, the answer is torus. The solid is produced by rotating a circle around an imaginary axis, but in this surface of revolution, the axis is outside the circle. The resulting shape is a ring torus. Other torus shapes are produced when the axis is touching or slightly inside the circle. Some really strange mathematical shapes are produced when the rotating plane of the circle is not quite round, or is itself rotating around a point in the plane.  A toroid is a ring or donut shaped solid produced by a surface of revolution not necessarily limited to a circle. For example, a square used in this manner will produce a ring that would be uncomfortable on your finger. A toroidal polyhedron is a torus constructed with or converted into flat surfaces, with the shape dependent on how many flat surfaces you use. Toroidal Polyhedron would be a cool name for a band.

Gömböc

You might remember Weebles -they wobble, but they don’t fall down. However, if the heavy weight in the bottom of the toy ever came loose, you had a Weeble that fell down. In 1995, Russian mathematician Vladimir Arnold questioned whether there could be a 3-dimensional shape that would always return to its original position without the help of internal weights. If a shape could be found that had as few as two points of equilibrium, one stable and one unstable, the shape would naturally return to balancing on the one stable point. For a long time, mathematicians thought the shape was impossible. But in 2006, Gábor Domokos and Péter Várkonyi developed the gömböc. This odd shape has only two points it could possibly balance upon, and the point on top is too “pointed” to be stable. So, if you roll a gömböc around, it will soon right itself, returning to an upright position because of its shape, not because of any internal irregularities. It’s a Weeble that doesn’t wear out! Objet Geometries made the first fabricated gömböcs. They were numbered as a limited series (inside, using transparent materials of the same density as the rest of the object) and professor Arnold was presented with number one. You can buy one of your own.

Spidron

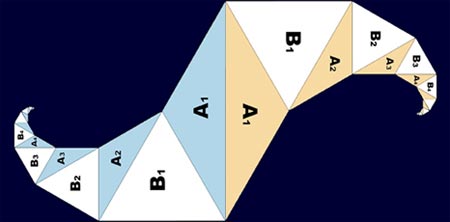
A spidron sounds like something that spins, and that’s what it looks like as well. A spidron is defined as a two-dimensional figure “consisting of an alternating sequence of equilateral and isosceles (30°, 30°, 120°) triangles.” OK, you know an equilateral triangle has three sides all the same length. An isosceles triangle doesn’t (the hypotenuse is longer). So when the equilateral triangle adjoins the right side of an triangle isosceles on one side and the hypotenuse on the other side, you see that the size of the isosceles triangles get smaller as they go on -and therefore the size of the equilateral triangle decreases as well. So the shape peters out as it grows longer, and it shifts a bit to the side because of the isosceles triangle shape. Since the shape grows in at least two directions (or it’s only a semi-spidron), the shape looks like a twisty pinwheel blade of sorts. But what good is it? Just take a look at how they fit together!

There are more spidron designs than can be contained in one post. See, with enough spidrons, any math whiz can be another M.C. Escher!

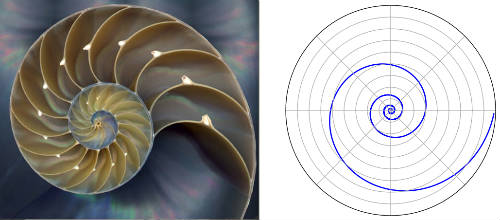
Bernoulli’s Spiral

Jacob Bernoulli was a Swiss mathematician who studied spirals produced by logarithms, which he called Spira mirabilis, or “the marvelous spiral”. These are often called Bernoulli’s spirals now in honor of the man who popularized them. There is a mathematical formula, but the simple explanation is that the spiral grows larger as it progresses outward, but the curve does not. This gives it a particular shape you may recognize in nature, most commonly in snail shells and seashells. You can also see logarithmic spirals in weather systems, spiral galaxies, and in flowers, in which case there are often spirals growing in opposite directions.

Mandelbrot Fractals

(Image credit: Wolfgang Beyer)

The word fractal has the same root as fracture, meaning broken. Fractals are geometric shapes that, if broken into parts, fracture into parts that are a smaller version of the whole (the same shape, that is) which is called a self-similar image. So those parts themselves are copies of the whole, and can be further broken down into smaller parts that are also copies of the whole. We non-math folks sometimes call this recursion. True fractals don’t exist in nature, as there is a limit to how small finite units can go -as far as we know, atoms only come in certain shapes. However, in geometry they can be broken down infinitely. A Mandelbrot set (named after mathematician Benoît Mandelbrot, who coined the term fractal) is a complex set of points on a plane that has a fractal boundary. In other words, the shape of the set repeats itself along the edge, and each repeating shape also contains repeating shapes, no matter how closely you zoom into the plane. This is easier to understand by looking at it.

(YouTube link)

That’s pretty mind-blowing by itself. Could a Mandelbrot set be made into a 3-dimensional shape?

Mandelbulb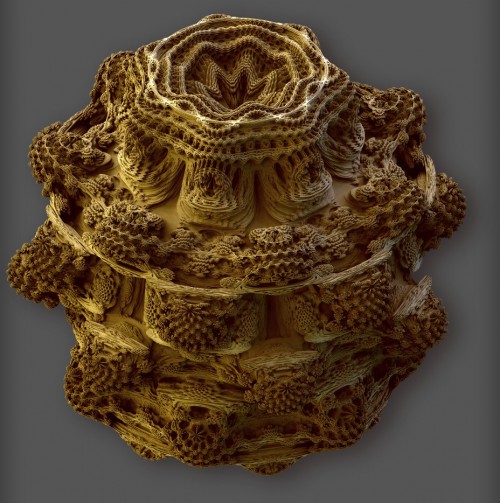

The Mandelbulb is a 3-dimensional representation of a Mandelbrot set. Daniel White set out to go beyond the idea of rotating a plane around an imaginary axis to create a 3-dimensional shape. He published an experimental formula to create a true 3D Mandelbrot set in 2007. Paul Nylander from Fractal Forums helped refine the formula. The resulting shape called a Mandelbulb is not quite what they are looking for -yet, but the two men are still working on perfecting the formula. See more pictures of the Mandelbulb here. No, I can’t even pretend to know how they accomplished that one, so with my mind adequately blown, I’ll end this list.

There are formulas for each of these shapes, which mean little if you aren’t at ease with higher geometry. If you are interested, you can find those formulas by following the links in this post.